Giải bài tập trang 130, 131 Ôn tập cuối năm đại số sgk toán 8 tập 2. Câu 1: Phân tích các đa thức sau thành nhân tử:…
Bài 1 trang 130 sgk toán 8 tập 2
Phân tích các đa thức sau thành nhân tử:
a)({a^2} – {b^2} – 4a + 4;)
Bạn đang xem: Giải bài 1, 2, 3, 4, 5 trang 130, 131 SGK toán 8 tập 2
b) ({x^2} + 2x – 3)
c) (4{x^2}{y^2} – {left( {{x^2}{y^2}} right)^2})
d) (2{a^3} – 54{b^3}) .
Hướng dẫn làm bài:
a) ({a^2} – {b^2} – 4a + 4 Leftrightarrow {a^2} – 4a + 4 – {b^2})
= ({left( {a – 2} right)^2} – {b^2} = left( {a – 2 + b} right)left( {a – 2 – b} right))
= (left( {a + b – 2} right)left( {a – b – 2} right))
b) ({x^2} + 2x – 3 = {x^2} + 2x + 1 – 4)
=({left( {x + 1} right)^2} – {2^2} = left( {x + 1 + 2} right)left( {x + 1 – 2} right))
=(left( {x + 3} right)left( {x – 1} right))
c) (4{x^2}{y^2} – {left( {{x^2}{y^2}} right)^2} = {left( {2xy} right)^2} – {left( {{x^2} + {y^2}} right)^2})
= (left( {2xy – {x^2} – {y^2}} right)left( {2xy + {x^2} + {y^2}} right))
=( – left( {{x^2} – 2xy + {y^2}} right)left( {{x^2} + 2xy + {y^2}} right))
=( – {left( {x – y} right)^2}{left( {x + y} right)^2})
d) (2{a^3} – 54{b^3} = 2left( {{a^3} – 27{b^3}} right))
=(2left[ {{a^3} – {{left( {3b} right)}^3}} right] = 2left( {a – 3b} right)left( {{a^2} + 3ab + 9{b^2}} right)).
Bài 2 trang 130 sgk toán 8 tập 2
a)Thực hiện phép chia:
(2×4 – 4×3 + 5×2 + 2x – 3) : (2×2 – 1).
b) Chứng tỏ rằng thương tìm được trong phép chia trên luôn luôn dương với mọi giá trị của x.
Hướng dẫn làm bài:
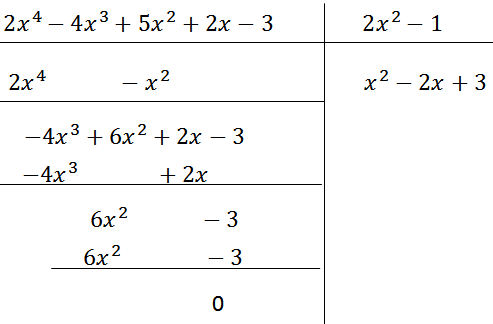
Vậy (2left[ {{a^3} – {{left( {3b} right)}^3}} right] = 2left( {a – 3b} right)left( {2{x^4} – 4{x^4} + 5{x^2} + 2x – 3} right):left( {2{x^2} – 1} right) = {x^2} – 2x + 3left( {{a^2} + 3ab + 9{b^2}} right))
Vậy (x in left{ { – 2;1;2;5} right})
b) Thương tìm được có thể viết:
({x^2} – 2x + 3 = left( {{x^2} – 2x + 1} right) + 2)
= ({left( {x – 1} right)^2} + 2 > 0) với mọi x
Vậy thương tìm được luôn luôn dương với mọi giá trị của x.
Bài 3 trang 130 sgk toán 8 tập 2
Chứng minh rằng hiệu các bình phương của hai số lẻ bất kì thì chia hết cho 8.
Hướng dẫn làm bài:
Gọi hai số lẻ bất kì là 2a + 1 và 2b + 1 (a, b ∈ Z)
Hiệu bình phương của hai số lẻ đó bằng :
({left( {2a{rm{ }} + {rm{ }}1} right)^2}-{rm{ }}{left( {2b{rm{ }} + {rm{ }}1} right)^2} = left( {4{a^2} + {rm{ }}4a{rm{ }} + {rm{ }}1} right){rm{ }}-{rm{ }}left( {4{b^2} + {rm{ }}4b{rm{ }} + 1} right))
( = left( {4{a^2} + {rm{ }}4a} right){rm{ }}-{rm{ }}left( {4{b^2} + {rm{ }}4b} right){rm{ }} = {rm{ }}4aleft( {a{rm{ }} + 1} right){rm{ }}-{rm{ }}4bleft( {b{rm{ }} + {rm{ }}1} right))
Vì tích của hai số nguyên liên tiếp luôn chia hết cho 2 nên a(a+1) và b(b+1) chia hết cho 2.
Do đó 4a(a + 1) và 4b(b + 1) chia hết cho 8
4a(a + 1) – 4b(b + 1) chia hết cho 8.
Vậy ({left( {2a{rm{ }} + {rm{ }}1} right)^2}-{rm{ }}{left( {2b{rm{ }} + {rm{ }}1} right)^2}) chia hết cho 8.
Bài 4 trang 130 sgk toán 8 tập 2
Rút gọn rồi tính giá trị của biểu thức sau tại (x = – {1 over 3}) :
(left[ {{{x + 3} over {{{left( {x – 3} right)}^2}}} + {6 over {{x^2} – 9}} – {{x – 3} over {{{left( {x + 3} right)}^2}}}} right]left[ {1:left( {{{24{x^2}} over {{x^4} – 81}} – {{12} over {{x^2} + 9}}} right)} right])
Hướng dẫn làm bài:
+Ngoặc vuông thứ nhất:
(left[ {{{x + 3} over {{{left( {x – 3} right)}^2}}} + {6 over {{x^2} – 9}} – {{x – 3} over {{{left( {x + 3} right)}^2}}}} right]{{x + 3} over {{{left( {x – 3} right)}^2}}} + {6 over {{x^2} – 9}} – {{x – 3} over {{{left( {x + 3} right)}^2}}})
(= {{x + 3} over {{{left( {x – 3} right)}^2}}} + {6 over {left( {x – 3} right)left( {x + 3} right)}} – {{x – 3} over {{{left( {x + 3} right)}^2}}}left[ {1:left( {{{24{x^2}} over {{x^4} – 81}} – {{12} over {{x^2} + 9}}} right)} right])
(={{{{left( {x + 3} right)}^2} + 6left( {x – 3} right)left( {x + 3} right) – {{left( {x – 3} right)}^2}} over {{{left( {x – 3} right)}^2}{{left( {x + 3} right)}^2}}})
(={{{x^3} + 9{x^2} + 27x + 27 + 6{x^2} – 54 – left( {{x^3} – 9{x^2} + 27x – 27} right)} over {{{left( {x – 3} right)}^2}{{left( {x + 3} right)}^2}}})
(={{24{x^2}} over {{{left( {x – 3} right)}^2}{{left( {x + 3} right)}^2}}})
(={{24{x^2}} over {{{left( {{x^2} – 9} right)}^2}}})
+Ngoặc vuông thứ hai:
(1:left( {{{24{x^2}} over {{x^4} – 81}} – {{12} over {{x^2} + 9}}} right) = 1:left[ {{{24{x^2}} over {left( {{x^2} – 9} right)left( {{x^2} + 9} right)}} – {{12} over {{x^2} + 9}}} right])
(=1:left( {{{24{x^2} – 12left( {{x^2} – 9} right)} over {left( {{x^2} – 9} right)left( {{x^2} + 9} right)}}} right))
(=1:{{12{x^2} + 108} over {left( {{x^2} – 9} right)left( {{x^2} + 9} right)}})
(=1.{{left( {{x^2} – 9} right)left( {{x^2} + 9} right)} over {12{x^2} + 108}})
(={{left( {{x^2} – 9} right)left( {{x^2} + 9} right)} over {12{x^2} + 108}})
(={{left( {{x^2} – 9} right)left( {{x^2} + 9} right)} over {12left( {{x^2} + 9} right)}})
(={{{x^2} – 9} over {12}})
Nên (left[ {{{x + 3} over {{{left( {x – 3} right)}^2}}} + {6 over {{x^2} – 9}} – {{x – 3} over {{{left( {x + 3} right)}^2}}}} right]left[ {1:left( {{{24{x^2}} over {{x^4} – 81}} – {{12} over {{x^2} + 9}}} right)} right])
(=left[ {{{x + 3} over {{{left( {x – 3} right)}^2}}} + {6 over {{x^2} – 9}} – {{x – 3} over {{{left( {x + 3} right)}^2}}}} right]{{24{x^2}} over {{{left( {{x^2} – 9} right)}^2}}}.{{{x^2} – 9} over {12}})
(= {{2{x^2}} over {{x^2} – 9}}left[ {1:left( {{{24{x^2}} over {{x^4} – 81}} – {{12} over {{x^2} + 9}}} right)} right])
Tại (x = – {1 over 3}) giá trị của biểu thức là:
({{2{{left( { – {1 over 3}} right)}^2}} over {{{left( { – {1 over 3}} right)}^2} – 9}} = {{2.{1 over 9}} over {{1 over 9} – 9}} = {{{2 over 9}} over { – {{80} over 9}}} = – {1 over {40}})
Bài 5 trang 131 sgk toán 8 tập 2
Chứng minh rằng:
({{{a^2}} over {a + b}} + {{{b^2}} over {b + c}} + {{{c^2}} over {c + a}} = {{{b^2}} over {a + b}} + {{{c^2}} over {b + c}} + {{{a^2}} over {c + a}})
Hướng dẫn làm bài:
Cách 1: Thực hiện phép cộng riêng từng vế:
VT: (={{{a^2}} over {a + b}} + {{{b^2}} over {b + c}}{{{a^2}left( {b + c} right)left( {c + a} right) + {b^2}left( {a + b} right)left( {c + a} right) + {c^2}left( {a + b} right)left( {b + c} right)} over {left( {a + b} right)left( {b + c} right)left( {c + a} right)}} + {{{c^2}} over {c + a}})
(={{{b^2}} over {a + b}} + {{{c^2}} over {b + c}} + {{{a^2}} over {c + a}})
Tử bằng:
(={a^2}left( {bc + ab + {c^2} + ac} right) + {b^2}left( {ac + {a^2} + bc + ab} right) + {a^2}left( {ab + ac + {b^2} + bc} right))
(={a^2}bc + {a^3}b + {a^2}{c^2} + {a^3}c + a{b^2}c + {a^2}{b^2} + {b^3}c + a{b^3} + ab{c^3} + a{c^3} + {b^2}{c^2} + b{c^3})
(={a^3}left( {b + c} right) + {a^2}left( {bc + {b^2} + {c^2}} right) + aleft( {{b^3} + {c^3} + {b^2}c + b{c^2}} right) + bcleft( {bc + {b^2} + {c^2}} right)left( 1 right)) (1)
VP: (={a^3}left( {b + c} right) + {a^2}left( {bc + {b^2} + {c^2}} right) + aleft( {{b^3} + {c^3} + {b^2}c + b{c^2}} right){{{b^2}left( {b + c} right)left( {c + a} right) + {c^2}left( {a + b} right)left( {c + a} right) + {a^2}left( {a + b} right)left( {b + c} right)} over {left( {a + b} right)left( {b + c} right)left( {c + a} right)}} + bcleft( {bc + {b^2} + {c^2}} right)left( 1 right))
(={b^2}left( {bc + ab + {c^2} + ac} right) + {c^2}left( {ac + {a^2} + bc + ab} right) + {a^2}left( {ab + ac + {b^2} + bc} right))
(={b^3}c + a{b^3} + {b^2}{c^2} + a{b^2}c + a{c^3} + {a^2}{c^2} + b{c^3} + ab{c^2} + {a^3}b + {a^3}c + {a^2}{b^2} + {a^2}bc)
(={a^3}left( {b + c} right) + {a^2}left( {bc + {b^2} + {c^2}} right) + aleft( {{b^3} + {c^3} + {b^2}c + b{c^2}} right) + bcleft( {bc + {b^2} + {c^2}} right)) (2)
So sánh (1) và (2) ta suy ra vế trái bằng vế phải. Vậy đẳng thức được chứng minh.
Cách 2: Xét hiệu hai vế
({a^3}left( {b + c} right) + {a^2}left( {bc + {b^2} + {c^2}} right) + aleft( {{b^3} + {c^3} + {b^2}c + b{c^2}} right) + bcleft( {bc + {b^2} + {c^2}} right){{{a^2}} over {a + b}} – {{{b^2}} over {a + b}} + {{{b^2}} over {b + c}} – {{{c^2}} over {b + c}} + {{{c^2}} over {c + a}} – {{{a^2}} over {c + a}})
(={{left( {a + b} right)left( {a – b} right)} over {a + b}} – {{left( {b + c} right)left( {b – c} right)} over {b + c}} + {{left( {c + a} right)left( {c – a} right)} over {c + a}})
(=a – b + b – c + c – a = 0)
Vậy ({{{a^2}} over {a + b}} + {{{b^2}} over {b + c}} + {{{c^2}} over {c + a}} = {{{b^2}} over {a + b}} + {{{c^2}} over {b + c}} + {{{a^2}} over {c + a}})
Nhận xét: Cách 2 nhanh gọn hơn cách 1.
Trường THPT Ngô Thì Nhậm
Đăng bởi: THPT Ngô Thì Nhậm
Chuyên mục: Giải bài tập
