Giải bài tập trang 87 bài Ôn tập chương III – Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy của tam giác Sách giáo khoa (SGK) Toán 7. Câu 63: Hãy so sánh góc ADC và góc AEB…
Bài 63 trang 87 sgk toán 7 tập 2
Cho tam giác ABC với AC < AB. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Vẽ các đoạn thẳng AD, AE.
a) Hãy so sánh góc ADC và góc AEB.
Bạn đang xem: Giải bài 63, 64, 65, 66 trang 87 SGK Toán 7
b) Hãy so sánh các đoạn thẳng AD và AE.
Hướng dẫn làm bài:
Trong ∆ABC, ta có AB > AC (gt) ⇒ (widehat {ACB} > widehat {ABC}) (1)
Từ (1) suy ra được: (widehat {AC{rm{E}}} < widehat {AB{rm{D}}}) (hai góc kề bù) (2)
– Trong tam giác cân ACE, ta có:
(widehat {AC{rm{E}}} = widehat {E{rm{A}}C}) và (widehat {A{rm{E}}C} + widehat {E{rm{A}}C} + widehat {AC{rm{E}}} = {180^0})
hay (widehat {AC{rm{E}}} = 2widehat {A{rm{E}}C} = {180^0} Rightarrow widehat {A{rm{E}}C} = {{{{180}^0} – widehat {AC{rm{E}}}} over 2}) (3)
– Tương tự, trong tam giác cân ABD, ta có:
(widehat {A{rm{D}}B} = {{{{180}^0} – widehat {AB{rm{D}}}} over 2}) (4)
– Mà (widehat {AC{rm{E}}} < widehat {AB{rm{D}}}) (do (2))
Từ (2), (3), (4) suy ra: ({{{{180}^0} – widehat {AC{rm{E}}}} over 2} > {{{{180}^0} – widehat {AB{rm{D}}}} over 2})
suy ra (widehat {A{rm{E}}C} > widehat {A{rm{D}}B}) hay (widehat {A{rm{E}}B} > widehat {A{rm{D}}C}) (đpcm)
b) Xét ∆AED, ta có: (widehat {A{rm{E}}B} > widehat {A{rm{D}}C}) . Suy ra AD > AE
Bài 64 trang 87 sgk toán 7 tập 2
Gọi MH là đường cao của tam giác MNP. Chứng minh rằng: Nếu MN < MP thì HN < HP và (widehat {NMH} < widehat {PMH}) (yêu cầu xét hai trường hợp: khi góc N nhọn và khi góc N tù).
Hướng dẫn làm bài:
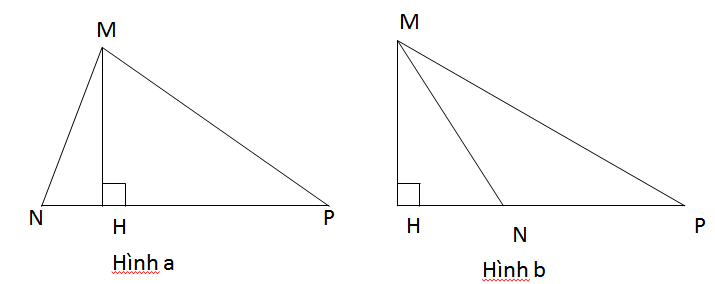
+Nếu góc N nhọn (hình a)
∆MNP có (hat N) nhọn nên chân đường cao H kẻ từ M nằm giữa N và P.
Ta có hình chiếu của MN và MP lần lượt là HN và HP.
Từ giả thiết MN < MP => HN < HP (quan hệ giữa các đường xiên và hình chiếu).
∆MNP có MN < MP => (widehat {MPN} < widehat {MNP}) (quan hệ giữa cạnh và góc trong tam giác)
Vì (widehat {NMH} + widehat {MNH} = {90^0}) (∆MNH vuông tại H)
(widehat {MPH} + widehat {PMH} = {90^0}$)(∆MHP vuông tại H)
Vậy (widehat {NMH} < widehat {PMH})
+Nếu góc N tù (hình b)
∆MNP có (hat N) tù nên chân đường cao H ở ngoài cạnh NP và N ở giữa H và P
=>HN < HP.
Vì N ở giữa H và P nên tia MN ở giữa hai tia MH và MP. Từ đó suy ra (widehat {HMN} < widehat {HMP})
Bài 65 trang 87 sgk toán 7 tập 2
Có thể vẽ được mấy tam giác (phân biệt) với ba cạnh là ba trong năm đoạn thẳng có độ dài như sau: 1cm, 2cm, 3cm, 4cm và 4cm?
Hướng dẫn làm bài:
Trong một tam giác, độ dài một cạnh lớn hơn hiệu và nhỏ hơn tổng của hai cạnh còn lại. Vậy nên với năm đoạn thẳng có độ dài 1cm, 2cm, 3cm, 4cm, 5cm chỉ dựng được tam giác với ba cạnh là các đoạn thẳng có độ dài là các bộ ba 2cm, 3cm, 4cm, bộ ba 3cm, 4cm, 5cm, bộ ba 2cm, 4cm, 5cm.
Bài 66 trang 87 sgk toán 7 tập 2
Đố: Bốn điểm dân cư được xây dựng như hình 58. Hãy tìm vị trí đặt một nhà máy sao cho tổng các khoảng cách từ nhà máy đến bốn điểm dân cư này là nhỏ nhất.
Hướng dẫn làm bài:
Gọi O là một điểm tùy ý (nơi phải đặt nhà máy) A, B, C, D lần lượt là bốn điểm dân cư.
Ta có:
+Nếu O nằm trên đoạn AC thì (left. {matrix{ {OA + OC = AC} cr {OB + OC = BD} cr } } right} = > OA + OB + OC + OD > AC + BD)
+Nếu O nằm trên đoạn BD thì (left. {matrix{ {OB + OD = BD} cr {OA + OC > AC} cr } } right} = > OA + OB + OC + OD > AC + BD)
+Nếu O không nằm trên AC và BD thì (left. {matrix{ {OA + OC > AC} cr {OB + OD > BD} cr } } right} = > OA + OB + OC + OD > AC + BD)
O là giao điểm của AC và BD thì (OA + OB + OC + OD = AC + BD)
-Vậy khi O là giao điểm của AC và BD thì tổng khoảng cách từ nhà nhà máy này đến các khu dân cư là ngắn nhất.
Trường THPT Ngô Thì Nhậm
Đăng bởi: THPT Ngô Thì Nhậm
Chuyên mục: Giải bài tập
