Giải bài tập trang 31, 32 bài 7 Giải bài toán bằng cách lập phương trình (tiếp) sgk toán 8 tập 2. Câu 45: Một xí nghiệp kí hợp đồng dệt một số tấm thảm len trong 20 ngày…
Bài 45 trang 31 sgk toán 8 tập 2
Một xí nghiệp kí hợp đồng dệt một số tấm thảm len trong 20 ngày. Do cải tiến kỹ thuật, năng suất dệt của xí nghiệp đã tăng 20%. Bởi vậy, chỉ trong 18 ngày, không những xí nghiệp đã hoàn thành số thảm cần dệt mà còn dệt thêm được 24 tấm nữa.Tính số tấm thảm len mà xí nghiệp phải dệt theo hợp đồng.
Hướng dẫn làm bài:
Bạn đang xem: Giải bài 45, 46, 47, 48, 49 trang 31, 32 SGK toán 8 tập 2
Gọi x là số tấm thảm len mà xí nghiệp phải dệt theo hợp đồng (x nguyên dương)
Số tấm thảm len mỗi ngày dự định dệt: ({x over {20}})
Số tấm thảm len thực tế đã dệt: x + 24
Số tấm thảm len mỗi ngày đã dệt:({{x + 24} over {18}})
Vì năng suất của xí nghiệp tăng 20% nên số thảm thực tế dệt trong một ngày bằng 120% số thảm dự định dệt trong một ngày; ta có phương trình:
({{x + 24} over {18}} = 120% .{x over {20}}) ⇔ ({{x + 24} over {18}} = {6 over 5}.{x over {20}})
⇔(50left( {x + 24} right) = 54x)
⇔(50x + 1200 = 54x)
⇔(4x = 1200)
⇔(x = 300) (thỏa điều kiện đặt ra).
Vậy số tấm thảm len dự định dệt là 300 tấm.
Bài 46 trang 31 sgk toán 8 tập 2
Một người lái ô tô dự định đi từ A đến B với vận tốc 48 km/h. Nhưng sau khi đi được một giờ với vận tốc ấy, ô tô bị tàu hỏa chắn đường trong 10 phút. Do đó, để kịp đến B đúng thời gian đã định, người đó phải tăng vận tốc thêm 6 km/h. Tính quãng đường AB
Hướng dẫn làm bài:
Gọi x là quãng đường AB (x > 0; km)
Đoạn đường đi trong 1 giờ: 48 km
Đoạn đường còn lại: x – 48
Thời gian dự đinh:({{x – 48} over {48}})
Thời gian thực tế:({{x – 48} over {54}})
Nếu không bị tàu hỏa chắn đường trong 10 phút thì ô tô sẽ đến sớm nên:
({{x – 48} over {48}} – {{x – 48} over {54}} = {1 over 6})
⇔(9left( {x – 48} right) – 8left( {x – 48} right) = 72)
⇔(9x – 432 – 8x + 384 = 72)
⇔(x = 120) (thỏa điều kiện đặt ra).
Vậy quãng đường AB bằng 120 km.
Bài 47 trang 32 sgk toán 8 tập 2
Bà An gửi vào quỹ tiết kiệm x nghìn đồng với lãi suất mỗi tháng là a% (a là một số cho trước) và lãi tháng này được tính gộp vào vốn cho tháng sau.
a)Hãy viết biểu thức biểu thị:
+Số tiền lãi sau tháng thứ nhất;
+Số tiền (cả gốc lẫn lãi) có được sau tháng thứ nhất;
+Tổng số tiền lãi có được sau tháng thứ hai.
b)Nếu lãi suất là 1,2% (tức là a = 1,2) và sau 2 tháng tổng só tiền lãi là 48,288 nghìn đồng, thì lúc đầu bà An đã gửi bao nhiêu tiền tiết kiệm?
Hướng dẫn làm bài:
a) Bà An gửi vào quỹ tiết kiệm: x đồng
Lãi suất là a% tháng nên số tiền lãi sau tháng thứ nhất a%.x
Số tiền lãi có được sau tháng thứ hai:
Tổng số tiền lãi sau hai tháng:
(a% x + left( {1 + a% } right)x.a% = left( {2 + a% } right).a% x)
b) Vì sau hai tháng bà An lãi 48288 đồng với lãi suất 1,2% nên:
(left( {2 + 1,2% } right)1,2% x = 48288 Leftrightarrow x = {{48288} over {2,012.0,012}})
⇔(x = 2000000)
Vậy bà An đã gửi tiết kiệm 2000 000 đồng.
Bài 48 trang 32 sgk toán 8 tập 2
Năm ngoái, tổng số dân của hai tỉnh A và B là 4 triệu. Năm nay, dân số của tỉnh A tăng thêm 1,1%, còn dân số của tỉnh B tăng thêm 1,2%. Tuy vậy, số dân của tỉnh A năm nay vẫn nhiều hơn tỉnh B là 807200 người. Tính số dân năm ngoái của mỗi tỉnh
Hướng dẫn làm bài:
Gọi x là số dân năm ngoái của tỉnh A (0 < x < 4 000 000; x ∈ N
Số dân tỉnh B: 4000 000 – x
Số dân của tỉnh A năm nay: 1,011.x
Số dân của tỉnh B năm nay: 1,012 (4000000 – x )
Vì dân số tỉnh A năm nay hơn tỉnh B là 8072000 người nên ta có phương trình:
(1,011x – 1,012left( {4000000 – x} right) = 807200)
⇔(1,011x – 4048000 + 1,012x = 807200)
⇔(2,023x = 4855200)
⇔ 9x = 2 400 000 (thỏa điều kiện đặt ra)
Vậy dân số của tỉnh A: 2 400 000 người
Dân số của tỉnh B: 1 600 000 người
Bài 49 trang 32 sgk toán 8 tập 2
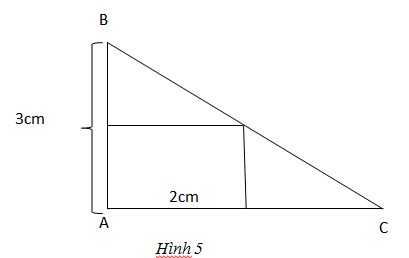
Đố: Lan có một miếng bìa hình tam giác ABC vuông tại A, cạnh AB = 3cm. Lan tính rằng nếu cắt từ miếng bìa đó ra một hình chữ nhật ấy có diện tích bằng một nửa diện tích của miếng bìa ban đầu. Tính độ dài cạnh AC của tam giác ABC.
Hướng dẫn làm bài:
Gọi x (cm) là cạnh AC (x > 0).
Gọi hình chữ nhật là MNPA thì MC = x – 2 (cm)
Vì MN // AB nên ({{MN} over {AB}} = {{MC} over {AC}})
=>(MN = {{AB.MC} over {AC}} = {{3left( {x – 2} right)} over x})
Diện tích hình chữ nhật : (2.{{3left( {x – 2} right)} over x} = {{6left( {x – 2} right)} over x})
Diện tích hình tam giác :({1 over 2}AB.AC = {1 over 2}.3x = {3 over 2}x)
Vì diện tích hình chữ nhật bằng một nửa diện tích hình tam giác
({3 over 2}x = 2{{6left( {x – 2} right)} over x} Leftrightarrow 3{x^2} = 24 – 48)
⇔(3{x^2} – 24x + 48 = 0)
⇔({x^2} – 8x + 16 = 0)
⇔({left( {x – 4} right)^2} = 0)
⇔(x = 4) (thỏa điều kiện đặt ra)
Vậy AC = 4cm.
Trường THPT Ngô Thì Nhậm
Đăng bởi: THPT Ngô Thì Nhậm
Chuyên mục: Giải bài tập
