Giải SGK Toán 7 trang 74 tập 1 Kết nối tri thức Bài luyện tập chung. Bài 4.19 Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz
Bài 4.16 trang 69 sách giáo khoa Toán 7 Kết nối tri thức tập 1
Cho hai tam giác ABC và DEF thoả mãn (AB = DE,AC = DF,widehat {BAC} = widehat {EDF} = {60^circ },BC = 6;{rm{cm}},widehat {ABC} = {45^circ }). Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.
Lời giải:
Bạn đang xem: Giải bài 4.16, 4.17, 4.18, 4.19 trang 74 SGK Toán 7 tập 1 – KNTT
Xét hai tam giác ABC và DEF có:
(begin{array}{l}AB = DEAC = DFwidehat {BAC} = widehat {EDF} = {60^circ }end{array})
(Rightarrow Delta ABC = Delta DEF)(c.g.c)
Do đó:
(EF = BC = 6cm)
(widehat {DEF} = widehat {ABC} = {45^o})
(begin{array}{l}widehat {BAC} + widehat {ABC} + widehat {ACB} = {180^o} Rightarrow {60^o} + {45^o} + widehat {ACB} = {180^o} Rightarrow widehat {ACB} = {75^o}end{array})
( Rightarrow widehat {EFD} = widehat {ACB} = {75^o})
Bài 4.17 trang 69 sách giáo khoa Toán 7 Kết nối tri thức tập 1
Cho hai tam giác ABC và DEF thoả mãn (AB = DE), (widehat {ABC} = widehat {DEF} = {70^circ },widehat {BAC} = widehat {EDF} = {60^circ },AC = 6;{rm{cm}}.)
Tính độ dài cạnh DF.
Lời giải:
Xét hai tam giác ABC và DEF có:
(begin{array}{l}widehat {ABC} = widehat {DEF} (= {70^circ })AB = DEwidehat {BAC} = widehat {EDF} (= {60^circ })end{array})
( Rightarrow Delta ABC{rm{ = }}Delta DEF)(g.c.g)
( Rightarrow DF = AC)( 2 cạnh tương ứng)
Mà AC = 6 cm
( Rightarrow DF = 6cm)
Bài 4.18 trang 69 sách giáo khoa Toán 7 Kết nối tri thức tập 1
Cho Hình 4.44, biết (EC = ED) và (widehat {AEC} = widehat {AED}). Chứng minh rằng:
(begin{array}{*{20}{l}}{{rm{ a) }}Delta AEC = Delta AED;}&{{rm{ b) }}Delta ABC = Delta ABD.}end{array})
Lời giải:

Bài 4.19 trang 69 sách giáo khoa Toán 7 Kết nối tri thức tập 1
Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz sao cho (widehat {CAO} = widehat {CBO}.)
a) Chứng minh rằng (Delta OAC = Delta OBC).
b) Lấy điểm (M) trên tia đối của tia CO. Chứng minh rằng (Delta MAC = Delta MBC).
Lời giải:
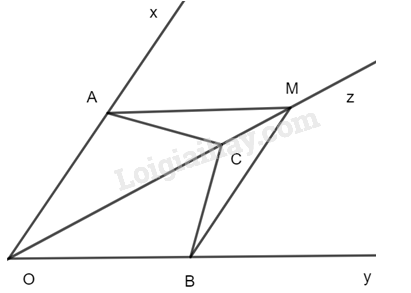
a)
Xét (Delta OAC) và (Delta OBC) có:
(widehat {AOC} = widehat {AOB})(Oz là phân giác góc xOy)
OC chung
(widehat {CAO} = widehat {CBO}.)
(Rightarrow Delta OAC = Delta OBC)(g.c.g)
b) Do (Delta OAC = Delta OBC) nên AC=BC ( 2 cạnh tương ứng)
Vì (widehat {ACO}) và (widehat {ACM}) kề bù
(widehat {BCO}) và (widehat {BCM}) kề bù
Mà (widehat {ACO} = widehat {BCO}) nên (widehat {ACM} = widehat {BCM})
Xét (Delta MAC) và (Delta MBC) có:
AC=BC
(widehat {ACM} = widehat {BCM})
CM chung
( Rightarrow Delta MAC = Delta MBC)(c.g.c)
Trường THPT Ngô Thì Nhậm
Đăng bởi: THPT Ngô Thì Nhậm
Chuyên mục: Giải bài tập
