Giải bài tập trang 119 bài 2 hình nón – hình nón cụt, diện tích xung quanh và thể tích của hình nón, hình nón cụt SGK toán 9 tập 2. Câu 23: Viết công thức tính nửa góc ở đỉnh của một hình nón…
Bài 23 trang 119 – Sách giáo khoa toán 9 tập 2
Bài 23 Viết công thức tính nửa góc ở đỉnh của một hình nón (góc (a) của tam giác vuông (AOS)- hình 99) sao cho diện tích khai triển mặt nón bằng một phần tư diện tích hình tròn (bán kính (SA)).
Bạn đang xem: Giải bài 23, 24, 25, 26 trang 119 SGK toán 9 tập 2
Giải:
Diện tích hình quạt :
(S_q = frac{pi r^2 n^o}{360^o}= frac{pi.l^2.90}{360}=frac{pi.l^2}4)
Diện tích xung quanh của hình nón: ({S_{xq}} = pi rl)
Theo đầu bài ta có: ({S_{xq}} = S_q )=> (πrl)= (frac{pi.l^2}4)
Vậy (l = 4r)
Suy ra (sin(a) )= (frac{r}l) =( 0,25)
Vậy (a = {14^0}28’)
Bài 24 trang 119 – Sách giáo khoa toán 9 tập 2
Bài 24. Hình khai triển mặt xung quanh của một hình nón là một hình quạt, bán kính hình quạt đó là (16cm), số đo cung là (120^0) Tan của góc ở đỉnh hình nón là:
(A) (frac{sqrt{2}}4) (B) (frac{sqrt{2}}2) (C) (sqrt{2}) (D) 2(sqrt{2})
Giải
Đường sinh của hình nón là (l = 16). Độ dài cung (AB) của đường tròn chứa hình quạt là(frac{32. pi}{3}) , chu vi đáy bằng suy ra (C= 2πr) suy (r) = (frac{16}{3})
Trong tam giác vuông (AOS) có: (h= sqrt{16^2- (frac{16}{3})^2}= 16sqrt{frac{8}{9}}= frac{32}{3}sqrt{2})
(tan(a)) = (frac{r}{h}) = (frac{sqrt{2}}{4})
Bài 25 trang 119 – Sách giáo khoa toán 9 tập 2
Bài 25. Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy (a,b) ((a
Giải:
Kí hiệu như hình vẽ. Ta có hai tam giác vuông (AO’C) và (AOB) đồng dạng vì có góc chung.
Nên (frac{l_1}{l – l_1}= frac{a}b) => (l_1 = frac{a}bl- frac{a}bl_1)
=> ((1+frac {a}b)l_1 = frac{a}{b}l) => (l_1 = frac{a}{a+b}l)
Diện tích xung quanh của hình nón lớn:
(S)xq nón lớn = (π.r.l =π.b.l)
Diện tích xung quanh của hình nón nhỏ:
(S)xq nón nhỏ =(pi .r.{l_1} = pi .a.{a over {a + b}}l = pi {{{a^2}} over {a + b}}l)
Diện tích xung quanh của hình nón cụt là:
(S)xq nón cụt = (S)xq nón lớn – (S)xq nón nhỏ
= (pi b l – pi frac{a^2}{a +b}l=(b-frac{a^2}{a+b})pi l)
= ((frac{b^2+ab- a^2}{a+b})pi l)
Bài 26 trang 119 – Sách giáo khoa toán 9 tập 2
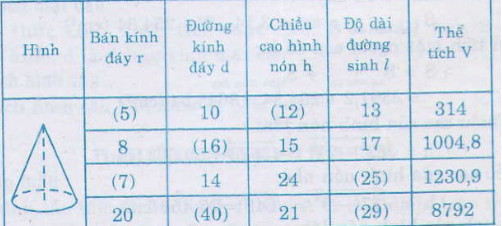
Bài 26 Hãy điền đầy đủ vào các ô trống cho ở bảng sau (đơn vị độ dài: cm):
Giải:
Dòng thứ nhất: (d = 2r =10)
(l = sqrt{h^2 + r^2}=sqrt{12^2+5^2}= sqrt{169}=13)
(V=frac{1}{3} pi r^2 h = frac{1}{3} 3,14 . 5^2 . 12 = 314)
Dòng thứ hai: (r = frac{d}{2} = 8)
(l = sqrt{h^2 + r^2}=sqrt{15^2+8^2}= sqrt{289}=17)
(V=frac{1}{3} pi r^2 h = frac{1}{3} 3,14 . 8^2 . 15 = 1004,8)
Các dòng thứ ba, thứ tư ta làm tương tự
Ta được bảng sau:
Trường THPT Ngô Thì Nhậm
Đăng bởi: THPT Ngô Thì Nhậm
Chuyên mục: Giải bài tập

