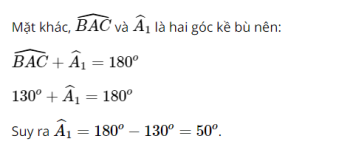Giải bài tập trang 132 Ôn tập cuối năm hình học sgk toán 8 tập 2. Câu 1: Dựng hình thang ABCD (AB// CD)…
Bài 1 trang 132 sgk toán 8 tập 2
Dựng hình thang ABCD (AB// CD), biết ba cạnh: AD = 2cm, CD = 4 cm, BC = 3cm và đường chéo AC = 5 cm.
Hướng dẫn làm bài:
Bạn đang xem: Giải bài 1, 2, 3, 4, 5 trang 132 SGK toán 8 tập 2
Dựng đoạn thẳng CD = 4cm.
-Dựng hai đường tròn (C; 5cm) và (D; 2cm) cắt nhau tại A.
-Dựng đường tròn (C; 2 cm) và đường tròn (A, 4cm) cắt nhau tại B.
Đường thẳng AB kéo dài cắt đường tròn (C, 2cm) tại điểm B’ (ngoài điểm B đã kể trên).
Các tứ giác ABCD và AB’CD là những hình thang thỏa mãn đề bài.
Chứng minh: Vì B ∈(A, 4cm) nên AB = 4cm.
∆ABC = ∆DAC (AB = CD = 4 cm, AD = BC = 2cm, AC chung) do đó là cặp góc so le trong ta có: AB // CD.
Tứ giác ABCD có AB // CD, AD = 2cm, CD = 4 cm, BC = 2 cm là hình thang thỏa mãn yêu cầu, AB’CD cũng là hình thang thỏa mãn yêu cầu vì AB’//CD, AD = 2cm, CD = 4 cm, CB’ = 2 cm).
Bài 2 trang 132 sgk toán 8 tập 2
Cho hình thang ABCD (AB // CD) có hai đường chéo cắt nhau ở O và tam giác ABO là tam giác đều. Gọi E, F, G theo thứ tự là trung điểm của các đoạn thẳng OA, OD và BC. Chứng minh rằng tam giác EFG là tam giác đều.
Hướng dẫn làm bài:
Tam giác ABO đều nên tam giác CDO cũng đều, suy ra OD = OC.
∆AOD = ∆BOC (c.g.c) =>AD = BC.
EF là đường trung bình của tam giác AOD nên:
(1) (EF = {1 over 2}AD = {1 over 2}BC) (1)
CF là đường trung tuyến của tam giác đều CDO nên CF ⊥ DO, nghĩa là .Trong tam giác vuông CFB, FG là đường trung tuyến ứng với cạnh huyền nên:
(2) (FG = {1 over 2}BC)
Chứng minh tương tự ta cũng có:
(3) (EG = {1 over 2}BC)
Từ (1), (2), (3) suy ra EF = GF = EG nên tam giác EFG là tam giác đều.
Bài 3 trang 132 sgk toán 8 tập 2
Tam giác ABC có các đường cao BD, CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau ở K. Tam giác ABC phải có điều kiện gì thì tứ giác BHCK là:
a) Hình thoi?
b) Hình chữ nhật?
Hướng dẫn làm bài:
Ta có: CE ⊥ AB(gt)
KB ⊥ AB (gt)
Suy ra BK // CH (1)
Tương tự BH // KC (2)
Từ (1) và (2) ta được :
Tứ giác BHCK là hình bình hành. Gọi M là giao điểm của hai đường chéo BC và HK.
a) BHCK là hình thoi HM ⊥ BC
Vì HA ⊥ BC nên HM ⊥ BC ⇔A, H, M thẳng hàng. Tam giác ABC cân tại A.
b) BHCK là hình chữ nhật ⇔ BH ⊥ HC. Ta lại có BE ⊥ HC, CD ⊥ BH nên BH ⊥ HC ⇔ H, D, E trùng nhau. Khi đó H, D, E cũng trùng với A. Vậy tam giác ABC là tam giác vuông ở A.
Bài 4 trang 132 sgk toán 8 tập 2
Cho hình bình hành ABCD. Các điểm M, N theo thứ tự là trung điểm của AB, CD. Gọi E là giao điểm của AN và DM, K là giao điểm của BN và CM. Hình bình hành ABCD phải có điều kiện gì để tứ giác MENK là:
a) Hình thoi?
b) Hình chữ nhật?
c) Hình vuông?
Hướng dẫn làm bài:
Tứ giác MBND là hình bình hành.
(MB// = ND)
Lại có MN // BC (vì MBCN là hình bình hành).
EK // CD (vì EK là đường trung bình của ∆CDM).
a) Để MENK là hình thoi thì hình bình hành MENK phải có hai đường chéo vuông góc. Tức là MN ⊥ EK.
Suy ra BC ⊥ CD.
Vậy ABCD phải là hình chữ nhật.
b) Để MENK là hình chữ nhật thì hình bình hành MENK phải có hai đường chéo bằng nhau. Tức là MN = EK.
Mà MN = BC, EK = ({1 over 2}CD) suy ra:
BC = ({1 over 2}) CD.
c) Để MENK là hình vuông thì MENK phải vừa là hình thoi vừa là hình chữ nhật. Tức là hình bình hành ABCD phải là hình chữ nhật có:
BC = ({1 over 2}DC)
Bài 5 trang 133 sgk toán 8 tập 2
Trong tam giác ABC các đường trung tuyến AA’ và BB’ cắt nhau ở G. Tính diện tích tam giác ABC biết rằng diện tích tam giác ABG bằng S.
Hướng dẫn làm bài:
Ta có: AC = 2AB’.
Nên SABC = 2SABB’ (1)
Và (BB’ = {3 over 2}BG)
Nên ({S_{ABB’}} = {3 over 2}{s_{ABG}}) (2)
Từ (1), (2) suy ra ({S_{ABC}} = 2.{3 over 2}{S_{ABG}} = 3S)
Trường THPT Ngô Thì Nhậm
Đăng bởi: THPT Ngô Thì Nhậm
Chuyên mục: Giải bài tập