Hình thoi là gì? Công thức tính diện tích và chu vi hình thoi, tính đường chéo hình thoi như thế nào. Mời bạn theo dõi bài viết của THPT Ngô Thì Nhậm chia sẻ dưới đây để cùng ôn lại và ghi nhớ các công thức cần thiết nhất liên quan đến hình thoi.
Hình thoi là gì?
Hình thoi là một tứ giác có 4 cạnh bằng nhau. Đây là hình bình hành có hai cạnh kề bằng nhau hay hình bình hành có hai đường chéo vuông góc với nhau.
Tính chất của hình thoi
- 2 góc đối bằng nhau
- 2 đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
- 2 đường chéo là các đường phân giác của các góc.
Bạn đang xem: Công thức tính diện tích hình thoi, chu vi hình thoi
Ở bài viết này, THPT Ngô Thì Nhậm sẽ giới thiệu lại các công thức tính diện tích và chu vi hình thoi hiệu quả cho việc học và công việc của bạn.
1. Công thức tính diện tích hình thoi
Diện tích hình thoi được đo bằng độ lớn của bề mặt hình, là phần mặt phẳng ta có thể nhìn thấy của hình thoi.
Công thức tính diện tích hình thoi dựa vào cạnh đáy và chiều cao
Diện tích của hình thoi bằng một nửa tích độ dài của hai đường chéo, công thức như sau:
Trong đó:
- S là diện tích hình thoi.
- d1 và d2 là hai đường chéo của hình thoi.
Ví dụ tính diện tích hình thoi.
Bài 1: Có một tấm bìa hình thoi đo được hai đường chéo cắt nhau có chiều dài lần lượt là 6 cm và 8 cm. Hỏi diện tích của tấm bìa hình thoi đó bằng bao nhiêu?
Áp dụng theo cách tính diện tích hình thoi, ta có d1 = 6 cm và d2 = 8 cm. Ta đưa vào công thức và có kết quả như sau:
S = 1/2 x (d1 x d2) = 1/2 (6 x 8) = 1/2 x 48 = 24 cm2
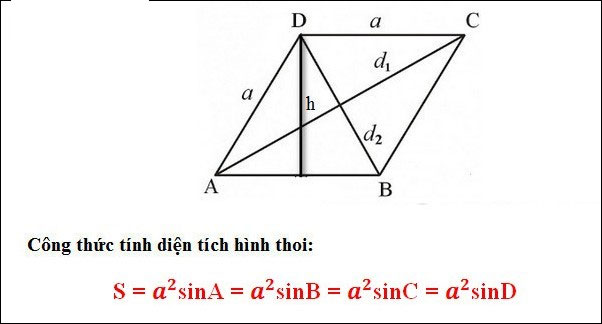
Công thức tính diện tích hình thoi dựa vào hệ thức trong tam giác (Nếu biết góc của hình thoi)
Trong đó: a: cạnh hình thoi
Ví dụ 1: Cho hình thoi ABCD, có cạnh hình thoi = 4cm, góc A = 35 độ. Tính diện tích hình thoi ABCD.
Giải: Áp dụng công thức, ta có a = 4, góc = 35 độ. Ta thay vào công thức như sau:
S = a2 x sinA = 42 x sin(35) = 9,176 (cm2)
Ví dụ 2:
Cho hình thoi ABCD có cạnh AD = 4m, có góc DAB = 30 độ. Tính diện tích của hình thoi ABCD.
Giải:
Do ABCD là hình thoi nên các tam giác tạo thành là tam giác cân, gọi I là trung điểm hai đường chéo nên AI vuông góc với BD, góc IAB = 15 độ.
Do đó, AI = AB. cos IAB = 4. Cos 15 = 3,84m.
Xét tam giác vuông ABI, theo định lý Pytago, ta có:
BI2= AB2- AI2= 1,25m
Nên BI = 1,1m
AC = 2. AI = 7,68m
BD = 2. BI = 2,2m
Dựa vào công thức tính diện tích hình thoi, ta có diện tích của hình thoi ABCD = ½ . AC . BD = 8,45(m2)
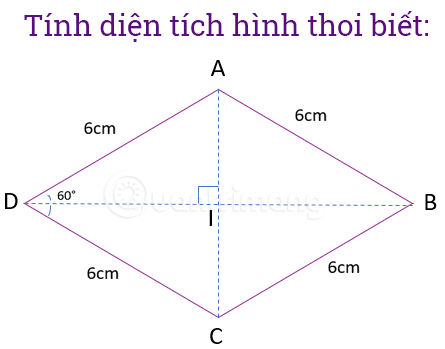
Ví dụ 3: Cho hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là 60°, hãy tính diện tích hình thoi.
Với những dữ kiện này bạn sẽ chưa có cơ sở gì để tính diện tích hình thoi. Bạn sẽ phải dựa vào tính chất hình thoi, tính chất tam giác đều, cách tính các cạnh trong một tam giác vuông để tính được đường chéo của hình thoi. Các bước làm như sau:
Bước 1: Vẽ hình và ghi chú các dữ kiện đã biết.
Bước 2: Vận dụng các tính chất của hình thoi ta có:
, đường chéo AC là phân giác của góc A, nên góc sẽ bằng 1/2 góc và bằng 60°. (Tổng các góc trong của tứ giác bằng 360°, tổng các góc trong của tam giác là 180°). Như vậy, tam giác ADC sẽ là tam giác đều => cạnh AC bằng 6cm. I là trung điểm AC => AI=3cm.
Bước 3: Tính độ dài DI
Tam giác DIA vuông tại I, cạnh DI sẽ tính như sau:
=> cm
Bước 4:Tính diện tích hình thoi ABCD:
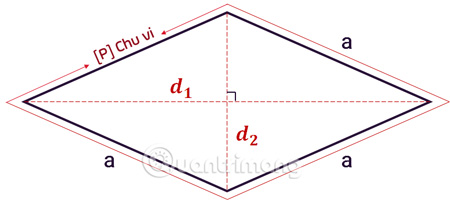
2. Công thức tính chu vi hình thoi
Chu vi hình thoi được tính bằng tổng độ dài các đường bao quanh hình, cũng chính là đường bao quanh toàn bộ diện tích.
Để tính chu vi hình thoi, ta tính tổng độ dài của 4 cạnh. Công thức cụ thể như sau:
Trong đó:
- P là chu vi hình thoi.
- a là chiều dài của cạnh hình thoi.
Ví dụ: Cho một hình thoi ABCD có độ dài các cạnh bằng nhau và bằng 7 cm. Hỏi chu vi của hình thoi này bằng bao nhiêu?
Theo công thức tính chu vi hình thoi được giới thiệu ở trên, ta có a = 7 cm. Như vậy chu vi hình thoi ABCD sẽ được tính như sau:
P (ABCD) = a x 4 = 7 x 4 = 28 cm
Nếu có thắc mắc gì liên quan đến công thức tính diện tích và chu vi hình thoi, hãy để lại comment bên dưới để cùng nhau trao đổi và giải đáp nhé. Cảm ơn các bạn đã theo dõi bài viết.
Đăng bởi: THPT Ngô Thì Nhậm
Chuyên mục: Tổng hợp