Giải bài tập trang 33 Ôn tập chương I – Phép nhân và phép chia các đa thức sgk toán 8 tập 1. Câu 80: Làm tính chia:…
Bài 80 trang 33 sgk toán 8 tập 1
Làm tính chia:
a) (left( {6{x^3} – 7{x^2} – x + 2} right):left( {2x + 1} right))
Bạn đang xem: Giải bài 80, 81, 82, 83 trang 33 SGK toán 8 tập 1
b) (left( {{x^4} – {x^3} + {x^2} + 3x} right):left( {{x^2} – 2x + 3} right)) ;
c) (left( {{x^2} – {y^2} + 6x + 9} right):left( {x + y + 3} right)) .
Hướng dẫn làm bài:
b) 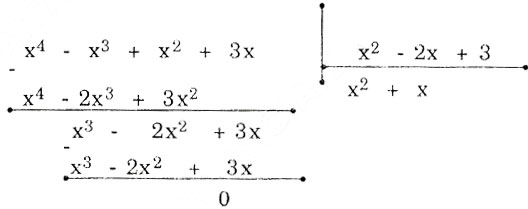
c) (left( {{x^2} – {y^2} + 6x + 9} right):left( {x + y + 3} right))
=(left( {{x^2} + 6x + 9 – {y^2}} right)left( {x + y + 3} right))
=(left[ {left( {{x^2} + 2x.3 + {3^2}} right) – {y^2}} right]:left( {x + y + 3} right))
=(left[ {{{left( {x + 3} right)}^2} – {y^2}} right]:left( {x + y + 3} right))
=(left( {x + 3 – y} right)left( {x + 3 + y} right):left( {x + y + 3} right))
= (x + 3 – y)
= (x – y + 3)
Bài 81 trang 33 sgk toán 8 tập 1
Tìm (x), biết:
a) ({2 over 3}xleft( {{x^2} – 4} right) = 0) ;
b) ({left( {x + 2} right)^2} – left( {x – 2} right)left( {x + 2} right) = 0) ;
c) (x + 2sqrt 2 {x^2} + 2{x^3} = 0) .
Giải
a) ({2 over 3}xleft( {{x^2} – 4} right) = 0)
({2 over 3}xleft( {{x^2} – {2^2}} right) = 0)
({2 over 3}xleft( {x – 2} right)left( {x + 2} right) = 0)
Hoặc (x = 0)
Hoặc (x – 2 = 0 Rightarrow x = 2)
Hoặc (x + 2 = 0 Rightarrow x = -2)
Vậy (x = 0,x = – 2,x = 2)
b) ({left( {x + 2} right)^2} – left( {x – 2} right)left( {x + 2} right) = 0)
(left( {x + 2} right)left[ {left( {x + 2} right) – left( {x – 2} right)} right] = 0)
(left( {x + 2} right)left( {x + 2 – x + 2} right) = 0)
(left( {x + 2} right).4 = 0)
(x + 2 = 0)
(x = – 2)
Vậy (x=-2)
c) (x + 2sqrt 2 {x^2} + 2{x^3} = 0)
(xleft( {1 + 2sqrt 2 x + 2{x^2}} right) = 0)
(x(1^2 + 2sqrt 2 x .1+ {left( {sqrt 2 x} right)^2}) = 0)
(x{left( {1 + sqrt 2 x} right)^2} = 0)
Hoặc (x = 0)
Hoặc ({left( {1 + sqrt 2 x} right)^2} = 0 Rightarrow 1 + sqrt 2 x = 0Rightarrow x = – {1 over {sqrt 2 }})
Vậy (x = 0,x = – {1 over {sqrt 2 }})
Bài 82 trang 33 sgk toán 8 tập 1
Chứng minh:
a) ({x^2} – 2xy + {y^2} + 1 > 0) với mọi số thực (x) và (y);
b) (x – {x^2} – 1 < 0) với mọi số thực (x).
Giải
a) ({x^2} – 2xy + {y^2} + 1 > 0) với mọi số thực (x) và (y)
Ta có ({x^2} – 2xy + {y^2} + 1 = left( {{x^2} – 2xy + {y^2}} right) + 1)
=({left( {x – y} right)^2} + 1 > 0) do ({left( {x – y} right)^2} ge 0) với mọi (x, y).
b) (x – {x^2} – 1 < 0) với mọi số thực (x).
Ta có (x – {x^2} – 1 = – left( {{x^2} – x + 1} right))
=( – left[ {{x^2} – 2.x.{1 over 2} + {{left( {{1 over 2}} right)}^2} + {3 over 4}} right])
= ( – left[ {{x^2} – 2x.{1 over 2} + {{left( {{1 over 2}} right)}^2}} right] – {3 over 4})
=( – {left( {x – {1 over 2}} right)^2} – {3 over 4} < 0) với mọi (x)
do ({left( {x – {1 over 2}} right)^2} ge 0) nên (-{left( {x – {1 over 2}} right)^2} le 0)
Bài 83 trang 33 sgk toán 8 tập 1
Tìm (n inmathbb Z) để (2{n^2} – n + 2) chia hết cho (2n +1).
Giải
Ta có: ({{2{n^2} – n + 2} over {2n + 1}} = {{2{n^2} + n – 2n – 1 + 3} over {2n + 1}})
=({{nleft( {2n + 1} right) – left( {2n + 1} right) + 3} over {2n + 1}} = {{left( {2n + 1} right)left( {n – 1} right) + 3} over {2n + 1}} = n – 1 + {3 over {2n + 1}})
Để (2{n^2} – n + 2) chia hết cho (2n + 1) (với (n inmathbb Z)) thì (2n + 1) phải là ước của (3). Do đó:
(2n + 1 = 1 = > 2n = 0 = > n = 0)
(2n + 1 = – 1 = > 2n = – 2 = > n = – 1)
(2n + 1 = 3 = > 2n = 2 = > n = 1)
(2n + 1 = – 3 = > 2n = – 4 = > n = – 2)
Vậy (n = 0; -1; -2; 1)
Trường THPT Ngô Thì Nhậm
Đăng bởi: THPT Ngô Thì Nhậm
Chuyên mục: Giải bài tập

