Giải bài tập trang 87, 88 bài 6 đối xứng trục Sách bài tập (SBT) Toán 8 tập 1. Câu 68: Trong các hình nét đậm vẽ trên giấy kẻ ô vuông ở hình 4, hình 5, hình nào có trục đối xứng ? …
Câu 68 trang 87 Sách bài tập (SBT) Toán 8 tập 1
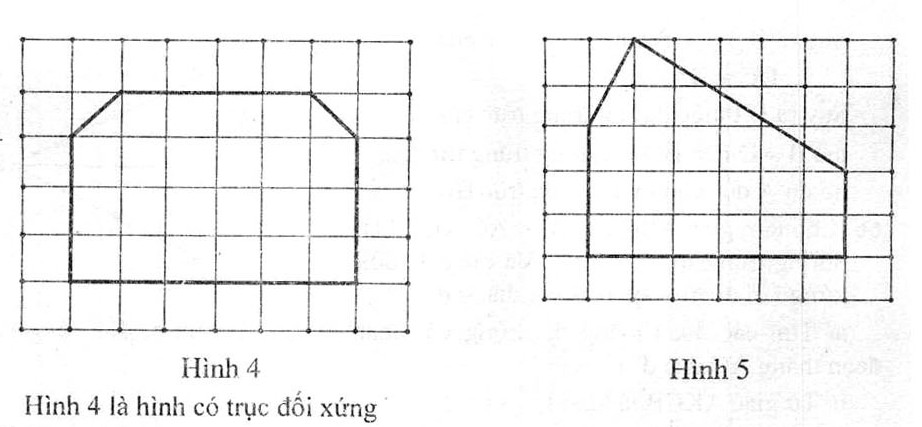
Trong các hình nét đậm vẽ trên giấy kẻ ô vuông ở hình 4, hình 5, hình nào có trục đối xứng ?
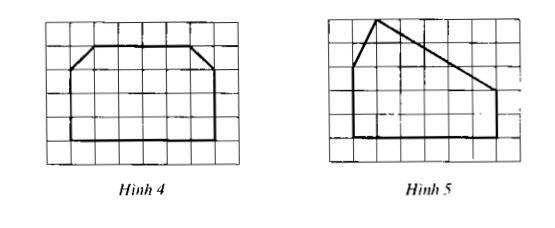
Bạn đang xem: Giải bài 68, 70, 71, 72 trang 87, 88 SBT Toán 8 tập 1
Giải:
Câu 70 trang 88 Sách bài tập (SBT) Toán 8 tập 1
Điền dấu “x” vào ô thích hợp:
Câu khẳng định Đúng Sai a. Tam giác có một trục đối xứng là tam giác cân b. Tam giác có một trục đối xứng là hình thang cân
Giải
Câu khẳng định Đúng Sai a. Tam giác có một trục đối xứng là tam giác cân x b. Tam giác có một trục đối xứng là hình thang cân x
Câu 71 trang 88 Sách bài tập (SBT) Toán 8 tập 1
Chứng minh rằng giao điểm hai đường chéo của hình thang cân nằm trên trục đối xứng của hình thang cân.
Giải:
Hình thang cân ABCD có AB // CD. Gọi O là giao điểm của hai đường chéo AC và BD.
Xét ∆ ADC và ∆ BCD:
AD = BC ( tính chất hình thang cân)
AC = BD ( tính chất hình thang cân)
CD cạnh chung
Do đó ∆ ADC = ∆ BCD (c.c.c)
( Rightarrow {widehat D_1} = {widehat C_1})
⇒ ∆ OCD cân tại O
⇒ OC = OD nên O nằm trên đường trung trực của CD.
Trục đối xứng của hình thang cân là đường thẳng trung trực của hai đáy.
Vậy O thuộc trục đối xứng của hình thang cân.
Câu 72 trang 88 Sách bài tập (SBT) Toán 8 tập 1
Cho góc nhọn xOy, điểm A nằm trong góc đó. Dựng điểm B thuộc tia Ox, điểm C thuộc tia Oy sao cho tam giác ABC có chu vi nhỏ nhất.
Giải:
Cách dựng:
– Dựng điểm D đối xứng với A qua Ox
– Dựng điểm E đối xứng với A qua tia Oy
– Nối DE cắt Ox tại B, Oy tại C
Tam giác ABC là tam giác có chu vi nhỏ nhất.
Vì (widehat {xOy} < {90^0}) nên DE luôn cắt Ox và Oy do đó ∆ ABC luôn dựng được.
Chứng minh:
Chu vi ∆ ABC bằng AB + BC + AC
Vì D đối xứng với A qua Ox nên Õ là đường trung trực của AD
⇒ AB = BD ( tính chất đường trung trực)
E đối xứng với A qua Oy nên Oy là đường trung trực của AE
⇒AC = CE ( tính chất đường trung trực)
Suy ra: AB + BC + AC = BD + BC + CE = DE (1)
Lấy B’ bất kì trên Ox, C’ bất kì trên tia Oy. Nối C’E, C’A, B’A, B’D.
Ta có: B’A = B’D ( tính chất đường trung trực)
C’A = C’E (tính chất đường trung trực)
Chu vi ∆ AB’C’ bằng AB’ + AC’ + B’C’ = B’D + B’C’ +C’E (2)
Vì DE ≤ B’D + B’C’ + C’E (dấu bằng sảy ra khi B’ trùng B. C’ trùng C)
nên chu vi của ∆ ABC ≤ chu vị của ∆ A’B’C’
Vậy ∆ ABC có chu vi bé nhất.
Trường THPT Ngô Thì Nhậm
Đăng bởi: THPT Ngô Thì Nhậm
Chuyên mục: Giải bài tập
