Giải bài tập trang 87 bài 6 đối xứng trục Sách bài tập (SBT) Toán 8 tập 1. Câu 64: Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm I, trên cạnh AC lấy điểm K sao cho AI = AK…
Câu 64 trang 87 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm I, trên cạnh AC lấy điểm K sao cho AI = AK. Chứng minh rằng điểm I đối xứng với điểm K qua AH.
Giải:
Bạn đang xem: Giải bài 64, 65, 66, 67 trang 87 SBT Toán 8 tập 1
∆ ABC cân tại A
AH ⊥ BC (gt)
Suy ra : AH là tia phân giác (widehat A)
AI = AK (gt)
⇒∆ AIK cân tại A
AH là tia phân giác (widehat A)
nên AH là đường trung trực của IK
Vậy I đối xứng với K qua AH.
Câu 65 trang 87 Sách bài tập (SBT) Toán 8 tập 1
Tứ giác ABCD có AB = BC, CD = DA (hình cái diều). Chứng minh rằng điểm A đối xứng với điểm C qua đường thẳng BD.
Giải:
Ta có: BA = BC (gt)
Suy ra b thuộc đường trung trực của AC
DC = DA (gt)
Suy ra D thuộc đường trung trực của AC
mà B ≠ D nên BD là đường trung trực của AC
do đó A đối xứng với C qua trục BD.
Câu 66 trang 87 Sách bài tập (SBT) Toán 8 tập 1
Tam giác ABC có AB < AC. Gọi d là đường trung trực của BC. Vẽ điểm K đối xứng với điểm A qua đường thẳng d.
a. Tìm các đoạn thẳng đối xứng với đoạn thẳng AB qua d, đối xứng với đoạn thẳng AC qua d.
b. Tứ giác AKCB là hình gì? Vì sao?
Giải:
a. d là đường trung trực của BC nên B và C đối xứng qua d
K đối xứng với A qua d
nên đoạn thẳng đối xứng với đoạn AB qua d là đoạn KC
Đoạn thẳng đối xứng với đoạn AC qua d là đoạn KB
b. d là đường trung trực của BC (gt)
⇒ d ⊥ BC
A và K đối xứng qua d nên d là trung trực của AK
⇒ d ⊥ AK
Suy ra: BC // AK. Tứ giác ABCK là hình thang
AC và KB đối xứng qua d nên AC = BK.
Vậy hình thang ABCK là hình thang cân.
Câu 67 trang 87 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C (M khác C). Chứng minh rằng AC + CB < AM + MB.
Giải:
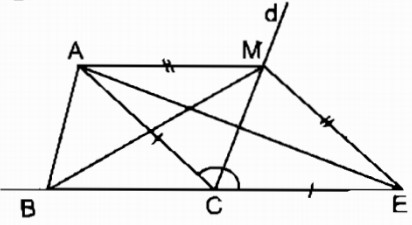
Trên tia đối tia CB lấy điểm E sao cho CE = CA. Nối MA, ME nên ∆ ACE cân tại C có CM là đường trung trực (tính chất tam giác cân)
⇒ MA = ME ( tính chất đường trung trực)
Ta có: AB + BC = BC + CE = BE (1)
MA + MB = MB + ME (2)
Trong ∆ MBE ta có: BE < MB + ME ( bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) suy ra: AB + BC = MA + MB
Trường THPT Ngô Thì Nhậm
Đăng bởi: THPT Ngô Thì Nhậm
Chuyên mục: Giải bài tập

