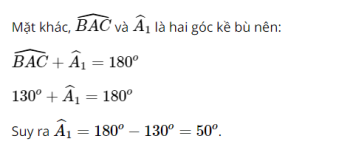Giải bài tập trang 74, 75 bài 3 Hình thang cân sgk toán 8 tập 1. Câu 11: Tính độ dài các cạnh của hình thang cân ABCD…
Bài 11 trang 74 sgk toán 8 tập 1
Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài cạnh ô vuông là 1cm).
Bài giải:
Bạn đang xem: Giải bài 11, 12, 13, 14, 15 trang 74, 75 SGK toán 8 tập 1
Theo hình vẽ, ta có: AB = 2cm, CD = 4cm
Trong tam giác vuông AED, áp dụng định lý Pitago ta được:
AD2 = AE2 + ED2
= 32 + 12 =10
Suy ra AD = (sqrt{10})cm
Vậy AB = 2cm, CD = 4cm, AD = BC = (sqrt{10})cm
Bài 12 trang 74 sgk toán 8 tập 1
Cho hình thang cân ABCD ( AB // CD, AB < CD). Kẻ đường cao AE, BF của hình thang. Chứng minh rằng DE = CF.
Bài giải:
Xét hai tam giác vuông AED và BFC
Ta có: AD = BC (gt)
(gt)
Nên ∆AED = ∆BFC (cạnh huyền – góc nhọn)
Suy ra: DE = CF
Bài 13 trang 74 sgk toán 8 tập 1
Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.
Bài giải:
Do ABCD là hình thang cân nên AD = BC, AC = BC, (widehat{D}=widehat{C})
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra (widehat{C_{1}}=widehat{D_{1}})
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, (widehat{D}=widehat{C}) , DC là cạnh chung.
Bài 14 trang 75 sgk toán 8 tập 1
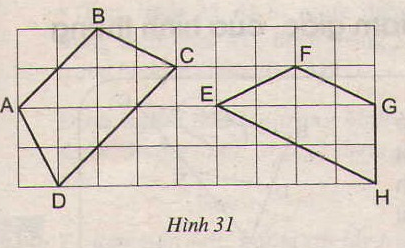
Đố. Trong các tứ giác ABCD và EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân? Vì sao?
Bài giải:
Để xét xem tứ giác nào là hình thang cân ta dùng tính chất
“Trong hình thang cân hai cạnh bên bằng nhau”
Tứ giác ABCD là hình thang cân vì có AD = BC.
Tứ giác EFGH không là hình thang cân vì EF > GH.
Bài 15 trang 75 sgk toán 8 tập 1
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D và E sao cho AD = AE.
a) Chứng minh rằng BDEC là hình thang cân.
b) Tính các góc của hình thang cân đó, biết rằng (widehat{A})=500
Bài giải:
a) Ta có AD = AE nên ∆ADE cân
Do đó (widehat{D_{1}}) = (widehat{E_{1}})
Trong tam giác ADE có: (widehat{D_{1}}) + (widehat{E_{1}}) + (widehat{A})=1800
Hay 2(widehat{D_{1}}) = 1800 – (widehat{A})
(widehat{D_{1}}) = (frac{180^{0}-widehat{A}}{2})
Tương tự trong tam giác cân ABC ta có (widehat{B}) = (frac{180^{0}-widehat{A}}{2})
Nên (widehat{D_{1}}) = (widehat{B}) là hai góc đồng vị.
Suy ra DE // BC
Do đó BDEC là hình thang.
Lại có (widehat{B}) = (widehat{C})
Nên BDEC là hình thang cân.
b) Với (widehat{A})=500
Ta được (widehat{B}) = (widehat{C}) = (frac{180^{0}-widehat{A}}{2}) = (frac{180^{0}-50^{0}}{2}) = 650
(widehat{D_{2}}=widehat{E_{2}})=1800 – (widehat{B})= 1800 – 650=1150
Trường THPT Ngô Thì Nhậm
Đăng bởi: THPT Ngô Thì Nhậm
Chuyên mục: Giải bài tập