Giải bài tập trang 58, 59 bài 1 Định lí Talet trong tam giác Sách giáo khoa toán 8 tập 2. Câu 1: Viết tỉ số của các cặp đoạn thẳng có độ dài như sau:…
Bài 1 trang 58 – Sách giáo khoa toán 8 tập 2
Viết tỉ số của các cặp đoạn thẳng có độ dài như sau:
a) AB = 5cm và CD 15 cm;
Bạn đang xem: Giải bài 1, 2, 3, 4, 5 trang 58, 59 SGK toán 8 tập 2
b) EF = 48 cm và GH = 16 dm;
c) PQ = 1.2m và MN = 24 cm.
Giải:
a) Ta có AB = 5cm và CD = 15 cm
<=> (frac{AB}{CD}) = (frac{5}{15}) = (frac{1}{3}).
b) EF= 48 cm, GH = 16 dm = 160 cm
<=> (frac{EF}{GH}) = (frac{48}{160}) = (frac{3}{10})
c) PQ= 1,2m = 120cm, MN= 24cm
<=> (frac{PQ}{MN}) = (frac{120}{24}) = 5.
Bài 5 trang 58 – Sách giáo khoa toán 8 tập 2
Tìm x trong các trường hợp sau(h.7):
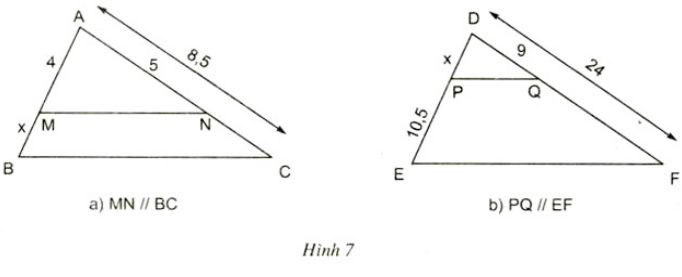
Giải:
a) MN // BC => (frac{BM}{AM}) = (frac{CN}{AN})
Mà CN = AN= 8.5 – 5= 3.5
nên (frac{x}{4}) = (frac{3.5}{5}) => x = (frac{4.3,5}{5}) = 1,4.
Vậy x = 1,4.
b)
PQ // EF => (frac{DP}{PE}) = (frac{DQ}{QF})
Mà QF = DF – DQ = 24 – 9 = 15
Nên
(frac{x}{10,5}) = (frac{9}{15}) => x = (frac{10,5.9}{15}) = 6,3
Bài 2 trang 59 – Sách giáo khoa toán 8 tập 2
Cho biết (frac{AB}{CD}) = (frac{3}{4}) và CD= 12cm. Tính độ dài AB.
Giải:
Ta có: (frac{AB}{CD}) = (frac{3}{4}) mà CD= 12cm nên
(frac{AB}{12}) = (frac{3}{4}) => A= (frac{12.3}{4}) = 9
Vậy độ dài AB= 9cm.
Bài 3 trang 59 – Sách giáo khoa toán 8 tập 2
Cho biết độ dài cùa AB gấp 5 lần độ dài của CD và độ dài của A’B’ gấp 12 lần độ dài của CD. Tính tỉ số của hai đoạn thẳng AB và A’B’.
Giải:
Độ dài AB gấp 5 lần độ dài CD nên AB= 5CD.
Độ dài A’B’ gấp 12 lần độ dài CD nên A’B’= 12CD.
=> Tí số của hai đoạn thẳng AB và A’B’ là:
(frac{AB}{A’B’})= (frac{5CD}{12CD}) = (frac{5}{12})
Bài 4 trang 59 – Sách giáo khoa toán 8 tập 2
Cho biết (frac{AB’}{AB}) = (frac{AC’}{AC}) (h.6)
Chứng minh rằng:
a) (frac{AB’}{B’B}) = (frac{AC}{C’C})’
b) (frac{BB’}{AB}) = (frac{CC’}{AC}).
Giải:
a) Ta có:
(frac{AB’}{AB}) = (frac{AC’}{AC}) => (frac{AC}{AC’}) = (frac{AB}{AB’})
=> (frac{AC}{AC’}) – 1 = (frac{AC-AC’}{AC’}) = (frac{AB-AB’}{AB’})
=> (frac{CC’}{AC’}) = (frac{B’B}{AB’}) => (frac{AB’}{BB’}) = (frac{AC’}{CC’})
b) Vì (frac{AB’}{AB}) = (frac{AC’}{AC}) mà AB’ = AB – B’B, AC’ = AC – C’C.
(frac{AB-BB’}{AB}) = (frac{AC -CC’}{AC}) => 1 – (frac{B’B}{AB}) = 1 – (frac{C’B}{AC})
=> (frac{B’B}{AB}) = (frac{C’B}{AC})
Trường THPT Ngô Thì Nhậm
Đăng bởi: THPT Ngô Thì Nhậm
Chuyên mục: Giải bài tập
